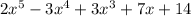We have the following polynomial:

Now, we can rewrite the polynomial in descending order as follows:
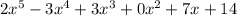
As we can see, the order in descending order takes into account the values for the exponents of the variable (an unknown value), x. Since the degree of a polynomial is the highest degree of any term of the polynomial, and this term is represented by:

In other words, the degree of a polynomial is the highest power we have for any term in the polynomial.
Therefore, the degree of the polynomial is 5, and we can write it, in descending order as follows:
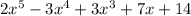
In summary, therefore, the degree of the polynomial is 5, in this case, and if we write it in descending order, we have: