Given:
a.) Jaz needs to have $5500 in 7 years.
b.) He will invest in a plan that pays 2.85%, compounded quarterly.
For us to be able to determine the principal amount needed to achieve $5500 in 7 years, we will be using the following formula:
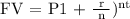
Where,
FV = future value = $5500
P = principal amount = money invested
r = interest rate (in decimal) = 2.85 ÷ 100 = 0.0285
n = number of times interest applied per time period = quarterly = 4
t = time (in years) = 7
We get,
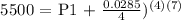
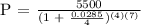
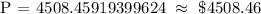
Therefore, Jaz will be needing to invest $4508.46 to achieve $5500 in 7 years.