Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).A professor is examining a new strain of bacteria. The amount of bacteria can be modeled by function s(n) = 20 · b^n, where n is the number of hours and b is an unknown positive base.

Answer 1

20 bacteria, 85%

Explanation:

We have that the function that models the situation is the following:

`\begin{gathered} s\left(n\right)=20·b^n \\ \\ b=1.85 \\ \\ \text{ Therefore:} \\ \\ s(n)=20\cdot(1.85)^n \end{gathered}`

An exponential equation has the following form:

`y=A_0\cdot(1+r)^n`

Where A0 is the initial value and r is the growth rate, therefore:

`\begin{gathered} A_0=20 \\ \\ 1+r=1.85 \\ \\ r=1.85-1=0.85 \\ \\ r=85\% \end{gathered}`

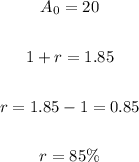
Therefore:

Based on model, there were initially 20 bacteria.

If b = 1.85, the hourly percent growth rate of the bacteria would be 85%