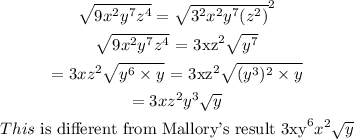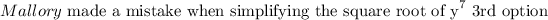Answer:
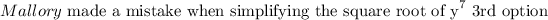
Step-by-step explanation:
Given:
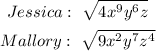
To find:
which student made an error in their simplification of the radical expression and what error they made
To determine the error made, we will solve each of the radial expressions and compare our result with Jessica and Mallory
Jessica:
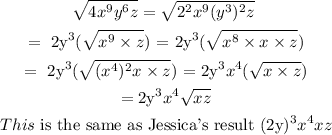
Mallory: