Given that the angles of the triangle are 30, 60, and 90.
Using the sine law
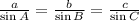
Substitute A=30, B=60, and C=90, we get
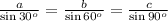
![\text{Substitute }\sin 30^o=(1)/(2),\sin 60^o=\frac{\sqrt[]{3}}{2},\text{ and }\sin 90^o=1,\text{ we get}](https://img.qammunity.org/2023/formulas/mathematics/high-school/mhel6t1y52iydcaf63zau834rptc959km9.png)
![(a)/((1)/(2))=\frac{b}{\frac{\sqrt[]{3}}{2}}=(c)/(1)](https://img.qammunity.org/2023/formulas/mathematics/high-school/1jjyqj7moc4a93onoml6e7pwshzcfn8ik6.png)
![2a=\frac{2b}{\sqrt[]{3}}=c](https://img.qammunity.org/2023/formulas/mathematics/high-school/mphh2ykmi1j7b804bzruzai6vqg3bzl1dh.png)
We know that the longest side should be the opposite side of the big angle (90).
Let c be the longest side of the given triangle.
Substitute c=1, we get
![2a=\frac{2b}{\sqrt[]{3}}=1](https://img.qammunity.org/2023/formulas/mathematics/high-school/pnj2o6tii9ll60gl9hst4lej3gn3q069qe.png)
![2a=1\text{ and }\frac{2b}{\sqrt[]{3}}=1](https://img.qammunity.org/2023/formulas/mathematics/high-school/s06h9vukweshxktxmr8836ehq4suxkoi79.png)
![a=(1)/(2)\text{ and }b=\frac{\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rf29mkc3tr6yef9p8ldz2ps6re6mm9a2yx.png)
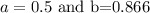
The smallest side is 0.5 feet
Conver the feet into inches.
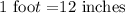
Dividing both sides by 2, we get
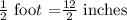
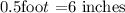
Hence the smallest side is 6 inches.