GIVEN:
We are given the following system of equations;

Required;
To determine whether or not the equations has a solution or no solution.
Step-by-step solution;
We can solve this system of equations by the elimination method. This is because none of the variables has 1 as its coefficient.
First step, we multiply equation (1) by -6 and then multiply equation (2) by 3 (that is, the coefficients of x in both equations).
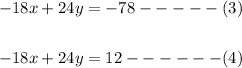
Next step, we subtract equation (4) from equatio (3);
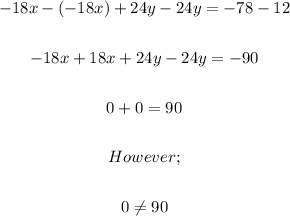
As we have seen from the calculations above, the result shows 0 equals 90 on both sides of the equality sign and that is NOT possible.
Therefore, for the given system of equations, there is NO SOLUTION
ANSWER:
Option B, that is 0 solutions is the correct answer.
Further Explanation;
For the graphs shown above, the color codes are as follows;
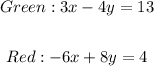
This simply tells us that for both equations, there is no point at which they can intersect and therefore,