Question

2. A 30-60-90 triangle has a hypotenuse of 10. Use special right triangle formulas to find the long side. Explain your work.

Answer 1

Given:

The angles of the triangle are in the order 30-60-90.

The hypotenuse side is 10.

To find:

The long side.

Step-by-step explanation:

Let us draw the triangle.

Using the trigonometric ratio formula,

`\begin{gathered} \sin\theta=(Opp)/(Hyp) \\ sin30^(\circ)=(Opp)/(10) \\ (1)/(2)=(Opp)/(10) \\ Opp=5 \end{gathered}`

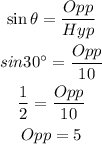
Using the trigonometric ratio formula,

`\begin{gathered} cos\theta=(Adj)/(Hyp) \\ cos60^(\circ)=(adj)/(10) \\ (√(3))/(2)=(adj)/(10) \\ adj=5√(3) \\ adj=8.66 \end{gathered}`

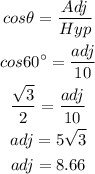
Comparing the three sides, the longest side will be the hypotenuse side.

That is side 10.

Final answer:

The longest side is the hypotenuse side of 10.