Question

How to labeling the y-intercept, vertex, and the axis of symmetry?

Answer 1

Answer:

• y-intercept = (0, 0)

,

• Vertex = (1/2, 5/4)

,

• Axis of symmetry = 1/2

Step-by-step explanation:

Given the function:

`f(x)=-5x^2+5x`

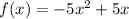
The vertex is:

`\begin{gathered} v_x=-(b)/(2a) \\ \\ \text{Where a = -5, b = 5} \\ \\ v_x=-(5)/(2(-5))=(1)/(2) \end{gathered}`

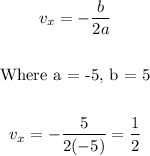
Substitute 1/2 into the given function to find the y-coordinate of the vertex

`\begin{gathered} v_y=-5((1)/(2))^2+5((1)/(2)) \\ \\ =(5)/(4) \end{gathered}`

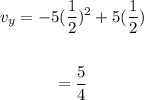
Therefore, the vertex is (1/2, 5/4)

Axis of symmetry:

This is -b/2a

`(1)/(2)`

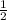
The y-intercept is (0, 0)