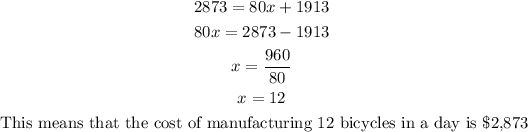Answer:
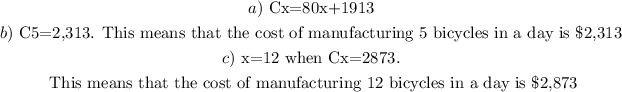
Explanation:
The situation is represented by a linear function since has an initial value or cost and it increases at a constant rate of change. Therefore, by the definition of a linear function:
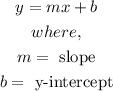
Therefore, if the daily fixed cost is $1913 and each bicycle costs $80 to manufacture:
a)
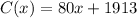
If x represents the number of bicycles manufactured, C(5) represents the cost of 5 bicycles manufactured in a day:
b)
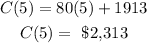
c) Find the value of x, substitute C(x)=2873