Given that the investment money is $700. The nominal annual interest rate is 4.5% and the time period is 11 years.
We have to find the amount at given time period.
a)
The formula when the interest is compounded annually is:
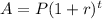
Substitute the given values in the formula:
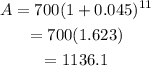
Thus, the answer is $1136.1.
b)
The formula of amount when the interest is compounded weekly is:
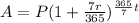
Substitute the given values in the formula:
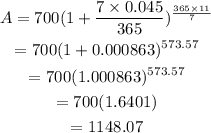
Thus, the answer is $1148.07.
c)
The formula of amount when the interest is compounded daily is:
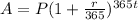
Substitute the given values in the formula:

Thus, the answer is $1147.86.
d)
The formula when the interest is compounded continuously is:
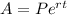
substitute the given values in the formula:
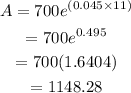
Thus, the answer is $1148.28.