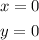Question

cises 12.5 slete the following: Find the intercepts and domain, and perform the symmetry test on each of the following ellipses. x² + 4y² = 36

Answer 1

Given the equation of the ellipse :

`x^2+4y^2=36`

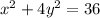
Divide the equation by 36:

`\begin{gathered} (x^2)/(36)+\frac{4y^{}2}{36}=(36)/(36) \\ \\ (x^2)/(36)+(y^2)/(9)=1 \\ \\ (x^2)/(6^2)+(y^2)/(3^2)=1 \end{gathered}`

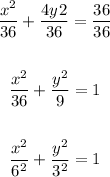
The last equation is similar to :

`(x^2)/(a^2)+(y^2)/(b^2)=1`

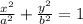
As a > b , the major axis will parallel to x - axis

`\begin{gathered} a=6 \\ b=3 \end{gathered}`

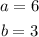
The vertices will represents x- intercepts =

`(-6,0),(6,0)`

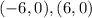
The y - intercepts will be :

`(0,-3),(0,3)`

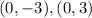
The axis of symmetry will be the lines :

`\begin{gathered} x=0 \\ y=0 \end{gathered}`