The variance is given by:
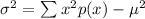
In this case the mean is equal to 4.9 so lets calculate the sum first:
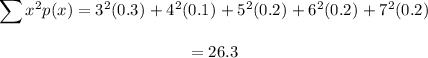
Now that we have the sum we plug it in the expression for the variance and the value of the mean:
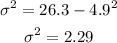
Therefore the variance is 2.3 (rounded to one decimal place)
The standard deviation is given by:
![\sigma=\sqrt[]{\sigma^2}](https://img.qammunity.org/2023/formulas/mathematics/college/1nil4daxtwmiiojjzy9q3k9t0m5jcp66vg.png)
Then in this case we have:
![\begin{gathered} \sigma=\sqrt[]{2.29} \\ \sigma=1.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mrevxr79f4fptaymmampsx9ym3ynjssshx.png)
Therefore the standard deviation is 1.5