Question

The Expression (x22) (x7) is equivalent to xp. What is value of p?

Answer 1

`(x^(22))(x^7)=x^p`

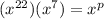
In the given expression the base value of the expression are same,

The genral form of base and exponent are given as :

`\begin{gathered} b^a,_{} \\ \text{here b is the base } \\ a\text{ = exponent value} \end{gathered}`

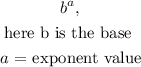
From the properties of base value,

If the base is same then the exponents value will add up,

`x^ax^{b^{}}=x^(a+b)`

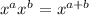
Since, we have

`\begin{gathered} (x^(22))(x^7)=x^p \\ \text{ so the exponents value will add up} \\ x^(22+7)=x^p \\ x^(29)=x^p \\ \text{bases are same, so compare the exponents value,} \\ 29=p \\ p=29 \end{gathered}`

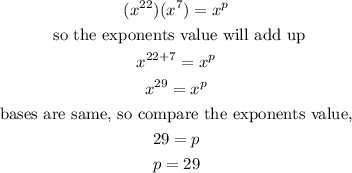
So, the value of p is 29.

Answer : p = 29