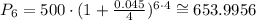To solve this problem we will use the formula for compound interest:
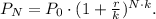
Where:
• P_N is the balance in the account after N years,
,
• P_0 is the starting balance of the account (also called an initial deposit, or principal),
,
• r is the annual interest rate in decimal form,
,
• k is the number of compounding periods in one year.
In this problem, we have that:
• N = 6 (6 years),
,
• P_N is the unknown,
,
• P_0 = 500,
,
• r = 4.5/100 = 0.045 (in decimals),
,
• k = 4 (because the interest compounded quarterly).
Replacing these values in the formula above, we find the following equation for this scenario: