Question

if you are solving for a missing SIDE round answer to hundredths place. if solving for and missing ANGLE round to the NEAREST DEGREE.

Answer 1

5) if the rocket is 300km high and 90km west, this are the legs, so we can use the trigonometric identity of tangent so:

`\tan (\theta)=(300)/(90)`

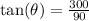
and we solve for theta so:

`\begin{gathered} \theta=\tan ^(-1)(3.3) \\ \theta=73.3º \end{gathered}`

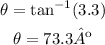
So the rocket was launch with an angle of 73º

6) In this problem wi have the high (210) and the hypothenuse (500) so we can use the identity of sin so:

`\sin (\theta)=(210)/(500)`

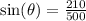
and we solve for theta so:

`\begin{gathered} \theta=\sin ^(-1)(0.42) \\ \theta=24.8º \end{gathered}`

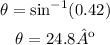
The angle of the mountan is 25º

7) the lenght of the ladder is 2.5m and the angle is 30, and we want to find the adyacent side so we use the cos identity so:

`\cos (30)=(x)/(2.5)`

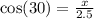
and we solve for x

`\begin{gathered} x=2.5\cos (30) \\ x=2.2 \end{gathered}`

so the ladder is 2.2m from the wall

8) the adyacent side is 600m and the angle is 28 so to find the high of the effiel towe we use the tangent identity so:

`\tan (28)=(x)/(600)`

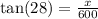
and we solve for x so

`\begin{gathered} x=600\tan (28) \\ x=319 \end{gathered}`

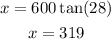
So the effiel tower is 319m