Question

A hair dryer with a resistance of 12.0 W and a lamp with a resistance of 125 W are connected in parallel to a 125-V source through a 1.50-W resistor in a series. Find the current through the lamp when the hair dryer is on.Question 2 options:1) 0.880 A2) 8.80 A3) 88.0 A4) 880 A

Answer 1

Given:

Resistance of hair dryer, R1= 12.0 Ohms

Resistance of lamp, R2 = 125 ohms

Voltage of source = 125 V

Resistance = 1.50 ohms

Let's find the curent through the lamp when the hair dryer is on.

Here, the lamp and dryer are connected in parralel. To calculate the equivalent resistance, apply the formula:

`\begin{gathered} (1)/(R_p)=(1)/(R_1)+(1)/(R_2) \\ \\ R_p=(R_1R_2)/(R_1+R_2) \\ \\ R_p=(12\ast125)/(12+125) \\ \\ R_p=(1500)/(137) \\ \\ R_p=10.9\text{ }\Omega \end{gathered}`

Now, the Rp and the resistor are connected in series.

To find the equivalent resistance in series, we have:

`\begin{gathered} R_(eq)=R_p+R \\ \\ R_(eq)=10.9+1.50=12.4\text{ }\Omega \end{gathered}`

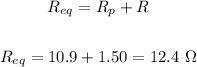
We now have a single resistor flowing through the 125 voltage source.

To find the current, apply Ohm's law:

`V=I\ast R`

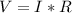
Solve for the current (I), where:

V = 125 volts

R = 12.4 Ω

Thus, we have:

`\begin{gathered} I=(V)/(R) \\ \\ I=(125)/(12.4)=10.1\text{ A} \end{gathered}`

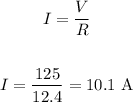
Since the resistor and Rp are connected in series, we have:

`\begin{gathered} V_p_{}=I_p\ast R_p \\ \\ V_p=10.1\ast10.9=110.1\text{ V} \end{gathered}`

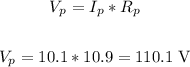
Since the dryer and the lamp are in parallel, the voltage through them are the same.

V(dryer) = V(lamp) = 110.1 Volts

To find the current flowing through the lamp, we have:

`\begin{gathered} I_{\text{lamp}}=\frac{V_(lamp)}{R_{\text{lamp}}} \\ \\ I_{\text{lamp}}=(110.1)/(125)=0.88\text{ A} \end{gathered}`

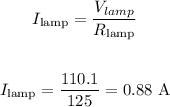
Therefore, the current through the lamp when the hair dryer is on is 0.880 ampere.

ANSWER:

1) 0.880 A