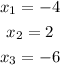We want to find the solutions for the following equation:

Since (x + 4) is a factor, we can rewrite this equation as a product of this factor by a second degree equation.
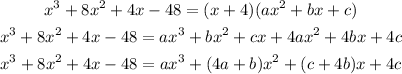
Comparing the coefficients from the left side with the coefficients from the right side, we get the following equations:
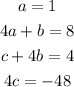
Solving this system, we get the following results:
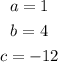
Rewriting our polynomial, we have
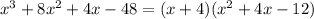
We can rewrite our original equation as
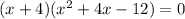
We have a product of two terms, then, if one is zero the product is zero.
To find the roots of this polynomial, we have to solve them individually
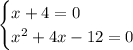
The solution for the first equation and the first root, is x = -4. Solving the second one we get the two remaining roots. We could solve it using the Bhaskara Formula, but I'm going to factorize it again using the same process.
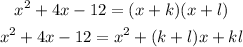
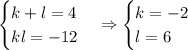
Our second degree polynomial can be rewritten as

This means our other roots are x = 2 and x = -6.