Question

Round your answer to two significant digits. Write your answer for the angle measure in decimal degrees.

Answer 1

Given: A right triangle with sides

`\begin{gathered} a=81\text{ mm} \\ c=99\text{ mm} \end{gathered}`

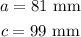
Required: To determine the measure of the angle

`\beta`

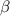
Explanation: The measure of the required angle can be determined by using the trigonometric ratio cosine as follows-

`cos\beta=(a)/(c)`

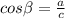
Substituting the values of a and b as-

`\begin{gathered} cos\beta=(81)/(99) \\ =(9)/(11) \end{gathered}`

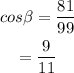
Hence, the angle is-

`\beta=cos^(-1)((9)/(11))`

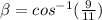
Thus-

`\begin{gathered} \beta=35.0968\degree \\ \beta\approx35.10\degree \end{gathered}`

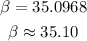
Final Answer: The measure of the angle is-