Given that the are of the great circle is 227 km^2.
The hemisphere is the half of a sphere, the surfsce area wiill be:
SA= (1/2)surface area of the sphere+ base area
the curve surface area will be:
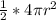
and we know that the base area is:
![\begin{gathered} BA=\pi r^2=227km^2 \\ r^2=(227km^2)/(\pi) \\ r=\sqrt[\placeholder{⬚}]{(227)/(\pi)}=8.5km \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/63pow5dss9c8z7se5e8rwq51w6jf2rkxfp.png)
substituting:
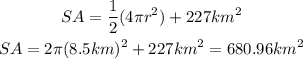
The surface area is: 680.96 square kilometers.