The given points are A(2,1) and P(3,3), where B is between A and P.
To find the x-coordinate of B, we use the following formula
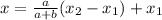
Where a=1 and b=4, using the given coordinates, we have
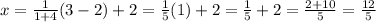
To find the y-coordinate of B, we use the following formula
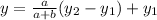
Replacing all values, we have
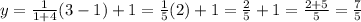
Therefore, point B is (12/5, 7/5).