The circle has center at teh origin ( 0,0) and a passing point ( -4, -3)
The general equation of circle is :
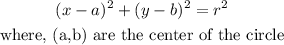
In the given question the center : ( 0,0)
So,
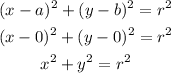
Since, the circle passes through ( -4, -3) so put x = -4 and y =-3 ans solve for r
![\begin{gathered} x^2+y^2=r^2 \\ (-4)^2+(-3)^2=r^2 \\ 16+9=r^2 \\ r^2=25 \\ r=\sqrt[]{25} \\ r=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/az1ik0jxhmtjj1q3e79exhxkr8lhhkuypl.png)
Thus radius = 5
Equation of circle is :
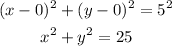
The general expression for the area pf circle is :
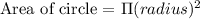
Substitute the value of radius = 5
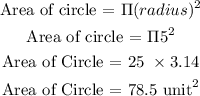
So, Area of circle is 78.5 unit²
Answer : Area of circle is 78.5 unit²