Question

Using the unpaid balance method, find the current months finance charge on a credit card account having the following transactions.

Last month’s balance: $385
Last payment: $250
Annual interest rate: 21%
Purchases: $303
Returns: $158
(It would be great if you could tell me how to use the formula I=Prt where previous months balance + finance charge + purchases made - returns - payments)

Answer 1

$5.02

Explanation:

The unpaid balance method is a common method used by credit card companies to calculate finance charges. It determines the finance charge based on a portion of the previous balance you have not yet paid.

Equations to use:

`\boxed{\begin{minipage}{9.7cm}\phantom{w}\\Periodic (monthly) rate = annual interest rate $/$ 12\\\\Finance Charge = previous balance $*$ periodic rate\\\\Unpaid Balance = previous balance + finance charge +\\\phantom{wwwwwwwwwww} new purchases - returns - payments\\\end{minipage}}`

The periodic rate is the interest rate charged over a certain number of time periods. The interest on a credit card is usually calculated monthly, so if the annual interest rate is 21%, then the periodic (monthly) rate is:

`\text{Periodic Rate}=(21\%)/(12)=1.75\%=0.0175`

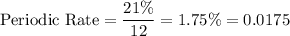
The unpaid balance is "last month's balance", which is $385.

Calculate the finance change by multiplying the previous balance (last month's balance) by the periodic rate:

`\begin{aligned}\text{Finance change} &=\rm previous\; balance * periodic\;rate \\&=\$385 * 0.0175 \\&= \$6.7375\end{aligned}`

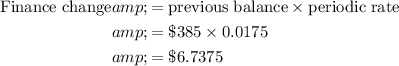
Calculate the unpaid balance by subtracting the returns and payments from the sum of the previous balance, finance charge and new purchases:

`\begin{aligned}\rm Unpaid \; Balance &= \rm previous\; balance + finance\;charge +new \;purchases\\&\phantom{=w}\rm - returns - payments\\&= \$385 + \$6.7375 + \$303 - \$158 - \$250 \\&= \$286.7375\end{aligned}`

Finally, to calculate the current month's finance charge, multiply the unpaid balance by the periodic rate:

`\begin{aligned}\text{Current month's finance charge}&=\rm unpaid \;balance* periodic \;rate\\&=\$286.7375 * 0.0175 \\&= \$5.02\; \text{(nearest cent)}\end{aligned}`

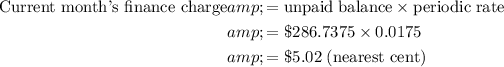
Therefore, the current month's finance charge is $5.02 to the nearest cent.