Question

Find the perimeter of the following. Put the steps in the order needed to solve this question.

Answer 1

In order to get the perimeter of a shape, we simply have to add the three sides of the triangle.

`5√(3)+4√(12)+3√(27)=Perimeter`

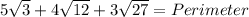
Now, numbers with radicals can be added if and only if they have the same index and radicand.

Looking at the dimensions of the triangle, they have the same index however, they do not have the same radicand. Therefore, we cannot add them right away. We have to convert each term in such a way that they have the same radicand.

Looking at the radicands, 3, 12, and 27, we can see right away that the common factor of the three numbers is 3. Thus, we can rewrite the equation above as:

`5√(3)+4√(4*3)+3√(9*3)=P`

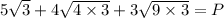
Then, we simply the radicands that are perfect square like 4 and 9. The square root of 1 is 1. The square root of 4 is 2. The square root of 9 is 3.

`\begin{gathered} (5*1√(3))+(4*2√(3))+(3*3√(3))=P \\ 5√(3)+8√(3)+9√(3)=P \end{gathered}`

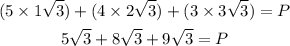
Now that they have the same radicand which is 3, we can now add the numbers by simply adding the whole numbers only. Then, copy the radicand.

`5√(3)+8√(3)+9√(3)=22√(3)`

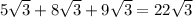
Therefore, the perimeter of the triangle is 22√3 units.