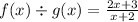Question

If AX) = 217 - x-6 and glx) = x2 - 4, find AX) = six).

Answer 1

Option C

`(2x+3)/(x+2)`

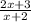
Step-by-step explanation

To find the division between two functions, first, we have to write the expression,

`f(x)/ g(x)=(2x^2-x-6)/(x^2-4)`

Then, to simplify, we have to factor each function by finding its zeros.

Function g(x) is a difference between two squares, so it can be factored as,

`g(x)=(x+2)(x-2)`

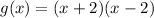
To find the zeros of function f(x) we can use the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \end{gathered}`

In this case, a = 2, b = -1, and c = -6,

`x=(-(-1)\pm√((-1)^2-4\cdot2\cdot(-6)))/(2\cdot2)=(1\pm√(1+48))/(4)=(1\pm√(49))/(4)=(1\pm7)/(4)`

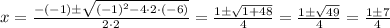
So, the zeros of f(x) are,

`\begin{gathered} x=(1+7)/(4)=(8)/(4)=2 \\ \\ x=(1-7)/(4)=(-6)/(4)=-(3)/(2) \end{gathered}`

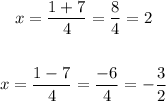
So, the factored form of f(x) is,

`f(x)=2(x-2)\left(x+(3)/(2)\right)`

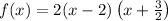
Replace each function by its factored form in the quotient,

`f(x)/ g(x)=(2(x-2)(x+(3)/(2)))/((x+2)(x-2))`

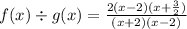
The factor (x - 2) is common in both numerator and denominator, so it cancels out,

`f(x)/ g(x)=(2(x+(3)/(2)))/(x+2)=(2x+3)/(x+2)`

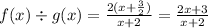
Hence, the quotient is,

`f(x)/ g(x)=(2x+3)/(x+2)`