Question

ABCD is a rectangle.A АB.AE =3+3DE = 50 - 15X =AC =Blank 1:Blank 2:

Answer 1

Since ABCD is a rectangle, then its diagonals are congruent and

`AE=EC=DE=CE`

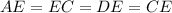
Graphically

• To find the value of x

We can write the following equation

`\begin{gathered} AE=DE \\ 3x+3=5x-15 \end{gathered}`

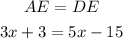
Now we can solve the equation for x

`\begin{gathered} \text{ Subtract 3 from both sides of the equation} \\ 3x+3-3=5x-15-3 \\ 3x=5x-18 \\ \text{ Subtract 5x from both sides of the equation} \\ 3x-5x=5x-18-5x \\ -2x=-18 \\ \text{ Divide by -2 from both sides of the equation} \\ (-2x)/(-2)=(-18)/(-2) \\ \boldsymbol{\mathbf{x=9}} \end{gathered}`

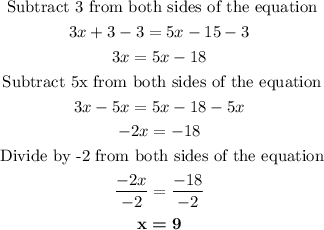
• To find the measure of AC

Since we know that

`\begin{gathered} AE=CE \\ \text{ Then} \\ AC=AE+CE \\ AC=AE+AE \\ AC=2\cdot AE \end{gathered}`

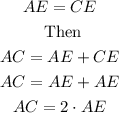
For which we only have to find the measure of AE. To do this, we replace the value of x in the given equation

`\begin{gathered} AE=3x+3 \\ AE=3\cdot9+3 \\ AE=27+3 \\ AE=30 \end{gathered}`

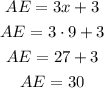
Finally, we have

`\begin{gathered} AC=2\cdot AE \\ AC=2\cdot30 \\ \boldsymbol{\mathbf{AC=60}} \end{gathered}`

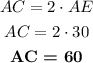
Therefore, the values of x and AC are

`\begin{gathered} x=9 \\ AC=60 \end{gathered}`