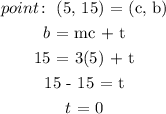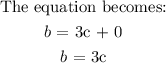Question

Fill in the blank for an equation to represent this problem. Use c for cans of paint and b for birdhouses painted.b= c

Answer 1

b = 3c

Step-by-step explanation:

let c = cans of paint = x

let b = birdhouses painted = y

To get equation for the values in the table, we would use equation of line:

y = mx + b

y in this case = b

x in this case = c

m = slope

We need to change the letter b for another to avoid confucion:

b = y-intercept

let y-intercept = t

The equation becomes:

b = mc + t

`\begin{gathered} \text{Slope formula:} \\ m\text{ = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }(b_2-b_1)/(c_2-c_1) \end{gathered}`
`\begin{gathered} u\sin g\text{ any two points:} \\ (5,\text{ 15) and (10, 30)} \\ x_1=5,y_1=15,x_2=10,y_2\text{ = }30 \\ m\text{ = }(30-15)/(10-5) \\ m\text{ = }(15)/(5)\text{ = 3} \end{gathered}`

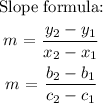
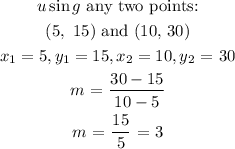
To get the y-intercept, we use slope and any of the two points:

`\begin{gathered} point\colon\text{ (5, 15) = (c, b)} \\ b\text{ = mc + t} \\ 15\text{ = 3(5) + t} \\ 15\text{ - 15 = t} \\ t\text{ = 0} \end{gathered}`
`\begin{gathered} \text{The equation becomes:} \\ b\text{ = 3c + 0} \\ b\text{ = 3c} \end{gathered}`