Answer:
x={0,1,6}
Given:
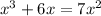
Let us first arrange the equation and equate it to 0
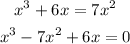
Factor out x:
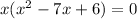
Then, factor out the quadratic equation inside the parenthesis using factoring:
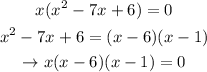
Now, we will equate each factor to 0 to find the solution to the equation
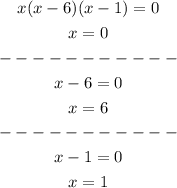
Therefore, the solutions to the equation is x={0,1,6}