Question

9. Express in simplest radical form with a rational denominator.

Answer 1

The given rational fraction is

`(√(49x^8))/(√(7x^3))`

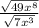
We will simplify it

First, simplify the numerator

Find the square root of 49 and the square root of x^8

`\begin{gathered} √(49)=7 \\ √(x^8)=x^{(8)/(2)}=x^4 \\ √(49x^8)=7x^4 \end{gathered}`

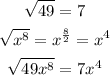
Now, simplify the denominator

Find the square root of x^3

`\begin{gathered} x^3=x* x* x \\ √(x^3)=√(x^2* x)=x√(x) \\ √(7x^3)=x√(7x) \end{gathered}`

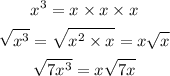
The fraction is

`(7x^4)/(x√(7x))`

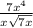
Simplify x^4 up with x down by subtracting their powers

`(7x^(4-1))/(√(7x))=(7x^3)/(√(7x))`

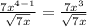
Multiply up and down by root 7x to rationalize the denominator

`\begin{gathered} (7x^3)/(√(7x))*(√(7x))/(√(7x))= \\ \\ (7x^3(√(7x)))/(7x)= \end{gathered}`

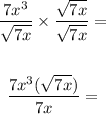
Simplify 7x^3 up with 7x down

`(7x^3)/(7x)=(7)/(7)x^(3-1)=1(x^2)=x^2`

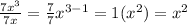
Then the simplest form is

`x^2√(7x)`

The answer is

`x^2√(7x)`