Question

1. College students on the honor roll average 38 hours of study time per week with a standard deviation of 90 minutes. If the study time is normally distributed, what percent of college students on the honor roll study more than 40 hours per week. Round to the nearest hundredth of a percent. Pay close attention to the units stated in the problem

Answer 1

we have the following:

The first thing is to pass the times to minutes

`\begin{gathered} 38h\cdot(60m)/(1h)=2280m \\ 40h\cdot(60m)/(1h)=2400m \end{gathered}`

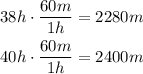
now, now to calculate the probability we must first calculate the value of z, as follows:

`z=\frac{x-\bar{x}}{sd}`

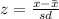
where x is 2400 minutes, the mean is 2280 minutes and sd is standard deviation equal 90 minutes, replacing:

`z=(2400-2280)/(90)=(4)/(3)=1.34`

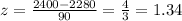
we look in the table of z, to what probability this value corresponds

and we can see that for that value of z, the probability is 0.9099 or what is equal to 90.99%.

Therefore, the answer is 90.99%