Answer:
855
Explanation:
Given the series:
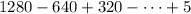
From observation, the series is geometric.

• The first term of the series, a = 1280
,
• The common ratio, r =-1/2
Since the series is finite, we find the number of terms in the series using the formula for the nth term of a geometric series:
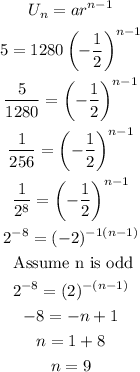
This means that there are 9 terms in the series.
For a geometric series with a common ratio of less than 1, the sum is calculated using the formula:
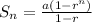
Substitute the values: a=1280, r=-1/2 and n=9
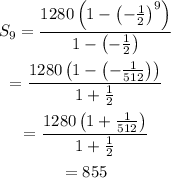
The sum of the series is 855.