Question

At a carnival, there is a raffle with 100 tickets. One ticket will win a $110 prize, fourteen tickets will win a $40 prize, seventeen tickets will win a $20 prize, and the other tickets will win nothing. If you have a ticket, what is the expected payoff? $

Answer 1

Expected Value of a Random Variable

Given a random variable X with possible values:

X={x1,x2,x3,...,xn}

With probabilities:

P={p1,p2,p3,...pn}

The expected value can be calculated as follows:

`Ex=\sum ^n_1x_i\cdot p_i`

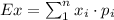
The distribution of the tickets is:

1 wins a $110 prize

14 win a $40 prize

17 win a $20 prize

The rest (100 - 1 - 14 - 17 = 68) win nothing.

The probabilities are:

p1=1/100 = 0.01

p2=14/100=0.14

p3=17/100=0.17

p4=68/100=0.68

Thus the sets are given as:

X={110,40,20,0}

And the probabilities:

P={0.01,0.14,0.17,0.68}

Calcuating the expected value:

Ex = 110*0.01 + 40*0.14 + 20*0.17 + 0*0.68

Ex = $10.10

The expected payoff is $10.10