Question

A girl works at a delicatessen, and it is her turn to make the zesty olive blend. If arbequina olives are $16 per pound and green olives are $25 per pound, how much of each kind of olive should she mix to get 9 pounds of zesty olive blend that will sell for $20 a pound?

Answer 1

Let's use the variable x to represent the number of pounds of arbequina olives and y to represent the number of pounds of green olives.

The final blend will have 9 pounds, so we have:

`x+y=9`

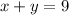
And the final price is $20 per pound, so we have:

From the first equation, we have y = 9 - x. Using this value of y in the second equation, we have:

`\begin{gathered} 16x+25(9-x)=180\\ \\ 16x+225-25x=180\\ \\ -9x=180-225\\ \\ -9x=-45\\ \\ x=5\\ \\ \\ \\ y=9-5=4 \end{gathered}`

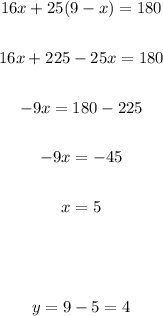
Therefore she needs 5 pounds of arbequina olives and 4 pounds of green olives.