To solve the system of equation graphically we need to plot each equation on the plane. First we notice that both equation are linear, which means that their graphs are lines; this also means that to graph them we just need two points for each equation. Let's graph the equations.
First equation: y=x-2
As we said we just need two points on the line, to get them we just need to give values to x (any values we want) and plug them in the equation to get y.
If x=0, then we have:
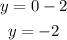
hence the line passes through the point (0,-2)
If x=1, then we have:

hence the line passes through the point (1,-1)
With this we conclude that the line passes through the points (0,-2) and (1,-1). Plotting this points on the plane and joining them with a straight line we have the graph of the first equation:
Second equation: y=-2x-5:
We follow the same procedure as with the first equation.
If x=0 we have:
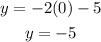
Hence the line passes through (0,-5)
If x=1 we have:
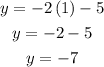
Hence the line passes through (1,-7)
Plotting this points and joining then with a line we have the graph for the second equation:
Finally, we plot both lines in the same plane. The solution of the system will be the point of intersection of the lines. The graph of the system is shown below:
From it we notice that the lines intersect at (-1,-3).
Therefore, the solution of the system is the point (-1,-3) which means that x=-1 and y=-3.