Question

Jamie has a rectangular pool that has a length of 12 feet and a

perimeter of 40 feet. What is the width of the pool?

Answer 1

The Width of the pool would be 8 feet/ft. .

Explanation:

According to the Question Given:

Perimeter = 40 ft/feet

Length of the pool = 12 ft/feet

To Find:

The width/breadth of the pool

Solution:

We know that,

`\boxed{\tt \: Perimeter \: of \: Rectangle = 2(l + b)}`

So Put their values accordingly:

• Perimeter of The Rectangle = 40
• Length[L] = 12

`\longrightarrow \tt \: 40 = 2(12 + b)`

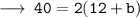
We got an equation.By this method we can easily find the breadth/width of the pool.

Solve this equation:

`\longrightarrow \tt40 = 2b + 24`

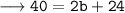
Flip the equation:

`\longrightarrow \tt2b + 24 = 40`

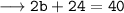
• Transpose 24 to the RHS[remember to change its sign]:

`\longrightarrow \tt2b = 40 - 24`

• Simplify:

`\longrightarrow \tt2b = 16`

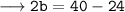
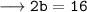
Divide both sides by 2:

`\tt\longrightarrow \cfrac{2b}{2} = \cfrac{16}{2}`

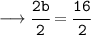
• Use Cancellation method and cancel LHS and RHS:

`\tt\longrightarrow \cfrac{ \cancel2 {}^(1) b}{ \cancel2} = \cfrac{ \cancel{16} {}^(8) }{ \cancel2}`

`\longrightarrow \tt1b = 8`

`\longrightarrow \tt{b} =\boxed{\tt 8 \: feet}`

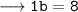
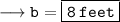
Hence, the breadth/width of the pool would be 8 ft./feet .

`\rule{225pt}{2pt}`

I hope this helps!

Answer 2

8 feet

Explanation:

Given,

Perimeter of a rectangular pool (P) = 40 feet

Length of the pool (l) = 12 feet

Let,

Width of the pool be = w

As we know,

• Perimeter of a rectangle = 2(length + width)

Therefore,

By the problem,

=> 2(l + w) = P

• [On substituting the values of l = 12 and P = 40]

=> 2(12 + w) = 40

• [On multiplying 2 with 12 and w]

=> 24 + 2w = 40

• [On subtracting both sides with 24]

=> 24 - 24 + 2w = 40 - 24

• [On Simplifying]

=> 2w = 16

• [On Dividing both sides with 2]

=>
`(2w)/(2)` =
`(16)/(2)`

• [On Simplifying]

=> w = 8

Hence,

The required width of the pool is 8 feet. (Ans)