x=3.2
Step-by-step explanation
As the figures are similar we can make a proporiton
so
Step 1
let
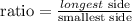
hence
for figure JKLM
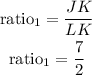
for figure PQRS

the ratio is the same, so the proportion is
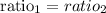
replace

Step 2
solve for x
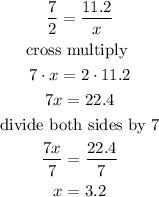
therefore, the answer is
x=3.2
I hope this helps you