Question

Contains the points (2,5) and (6, 21); slope-intercept form

Answer 1

In order to find the line equation, first consider that you can write the general equation of a line as follow:

y - yo = m(x - xo)

where m is the slope and (xo,yo) is any point on the line.

Calculate the slope m by using the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

where (x1,y1) and (x2,y2) are any points on the line.

In this case, you have:

(x1,y1) = (2,5)

(x2,y2) = (6,21)

Replace the previous values of the parameters into the formula for m:

`m=(21-5)/(6-2)=(16)/(4)=4`

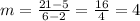
Now, use (xo,yo) = (2,5) and the previous value of m into the general equation for a line, and then solve for y, as follow:

`\begin{gathered} y-5=4(x-2) \\ y-5=4x-8 \\ y=4x-8+5 \\ y=4x-3 \end{gathered}`

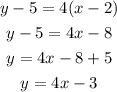
The previous result is the required equation in slope-intercept form.