Question

The row numbers y and column numbers x of a chessboard are shown. Each position on the chessboard has a stack of pennoes. The number of pennoes kn each stack is 2^x * 2^y a. Which locations have 32 pennies in their stacks? Write the coordinates in order from the point with the smallest x-value point with the largest x-value point b. How much money (in mdollars) is in the location with the tallest stack? There is $_ in the location with the tallest stack. c. A penny is about 0.06 inch thick. about how tall is the tallest stack? The tallest stack is about _ inches tall

Answer 1

The number of rows is represented by y and the number of columns is represented by x. The equation for the number of pennies in each stack is,

`\text{ 2}^x\text{ }\cdot2^y`

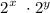
A.) To be able to locate the points that could stack 32 pennies, the equation below must be satisfied,

`\text{ 2}^x\cdot2^y\text{ = }32\text{ }\rightarrow2^x\cdot2^y=2^5\text{ }\rightarrow2^{x\text{ +y}}=2^5`

Let's equate the exponents since the bases are equal. We get,

`\text{ x + y = 5}`

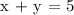
This equation means that the sum of x and y must be equal to 5. Thus, let's locate the combinations of x and y that is equal to 5 because these points could stack 32 pennies. We get,

`\text{ }(1,4),\text{ (2,3), }(3,2)\text{ and (4,1)}`

B.) How much money (in dollars) is in the location with the tallest stack?

A chessboard has maximum rows and columns of 8, thus, the location with the tallest stack must be (8,8).

Let's now compute the equivalent money of this stack in Dollar. Take note that 1 Pennie = 0.01 Dollar.

`\text{ 2}^8\text{ }\cdot2^8\text{ }\rightarrow2^{8\text{ + 8}}\text{ }\rightarrow2^(16)`
`\text{ = 65, 536 = 65, 536 Pennies}`

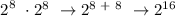
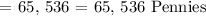
Converting into Dollar,

`\text{ 65, 536 (Pennies) x }\frac{0.01\text{ Dollar}}{1\text{ (Pennie)}}\text{ = 65, 536 x 0.01}`
`\text{ = 655.36 Dollars}`

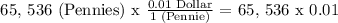
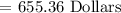
The tallest stack at (8,8) is equivalent to $ 655.36.

C.) A penny is about 0.06 inches thick. about how tall is the tallest stack?

`\text{ Thickness of Tallest Stack = 65, 536 (Pennies) x }\frac{0.06\text{ Inches}}{1\text{ (Pennie)}}`
`\text{ = 65, 536 x .06 Inches = 3, 932.16 Inches}`

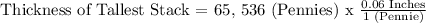
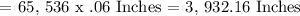
The tallest stack is about 3,932.16 inches tall.