Question

One positive number is 5 times another number. The difference between the twonumbers is 148. Find the numbers.0 20 and 100O 37 and 1850 1 and 5O 50 and 250

Answer 1

Let L and M represent two positive numbers.

Since one positive number is 5 times another number, we can make the statement:

`L=5M`

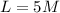
Since the difference between those numbers is 148, we can write down:

`L-M=148`

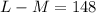
Where we have chosen L-M instead of M-L since L is greater than M and both are positive numbers (by using M-L, the difference would be negative).

Substitute 5M for L in the second equation:

`5M-M=148`

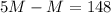
Solve for M:

`\begin{gathered} 4M=148 \\ \Rightarrow M=(148)/(4) \\ \Rightarrow M=37 \end{gathered}`

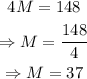
Once knowing M, multiply by 5 to get L:

`\begin{gathered} L=5\cdot37 \\ =185 \end{gathered}`

Therefore, those two numbers are 37 and 185.