Question

Suppose the half-life of a decaying radioactive isotope is 674 years. How long will it takefor the isotope to decay from 100 grams to 30 grams? Answer to the nearest hundredthof a year.accc

Answer 1

The half life formula is :

`N(t)=N_o((1)/(2))^{(t)/(T)}`

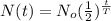
where N(t) = remaining quantity after t years

No = Original Quantity

t = time in years

T = half life in years

From the problem, we have :

N(t) = 30 grams

No = 100 grams

T = 674

Solve for t :

`\begin{gathered} 30=100((1)/(2))^{(t)/(674)} \\ (30)/(100)=((1)/(2))^{(t)/(674)} \\ (3)/(10)=((1)/(2))^{(t)/(674)} \end{gathered}`

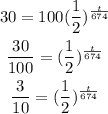
Take ln of both sides :

`\begin{gathered} \ln ((3)/(10))=\ln ((1)/(2))^{(t)/(674)} \\ \ln ((3)/(10))=(t)/(674)\ln ((1)/(2)) \\ t=(674\ln ((3)/(10)))/(\ln ((1)/(2))) \\ t=1170.71 \end{gathered}`

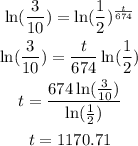
The answer is t = 1170.71 years