Question

The scatter plot below represents the depth of water in a tidal area over a 24-hour period.A. Determine the algebraic model if we use sine to model the depth of water over time.B. What would the depth of the water be at 4 hours? 30 hours?

Answer 1

The sine equation is given below as

`y=Asin(B(x+C)+D`

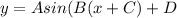
From the graph, The highest point on the crest is

`=5.5`

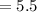
The lowest point of the trough is

`=0.5`

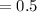
Hence,

The amplitude will be

`\begin{gathered} A=(5.5-0.5)/(2) \\ A=(5)/(2) \\ A=2.5 \end{gathered}`

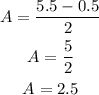
From the image also, the period T, is

`\begin{gathered} T=18 \\ T=(2\pi)/(B) \\ 18=(2\pi)/(B) \\ B=(2\pi)/(18) \\ B=(\pi)/(9) \end{gathered}`

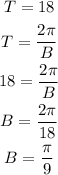
There is no hrizontal shift,

Hence,

The value of C is

`C=0`

The vertical shift D, will be

`D=3`

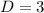
Hence,

The model of the sine function is given below as

`y=2.5\sin\left((\pi)/(9)x\right)+3`

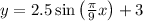
To figure out the depth at t=4hours, we will have substitue x=4 in the equation above

`\begin{gathered} y=2.5\sin((\pi)/(9)x)+3 \\ y=2.5\sin\mleft((\pi)/(9)*4\mright)+3 \\ y=5,462m \end{gathered}`

Hence,

The depth of the water at 4 hours is = 5.462m

To figure out the depth at t= 30 hours, we will have to substitute the value of x=30 in the equation above

`\begin{gathered} y=2.5\sin((\pi)/(9)x)+3 \\ y=2.5\sin\mleft((\pi)/(9)*30\mright)+3 \\ y=0.835m \end{gathered}`

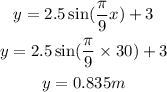
Hence,

The depth of the water at 30 hours is = 0.835m