Second-degree Equation
The second-degree equation is graphically represented as a curve called a parabola.
The parabola can be described by its vertex and leading coefficient as follows:

It's recognized the vertex form of the parabola needs to be expressed as the square of a binomial.
We are given the equation:
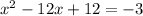
We need to complete squares to express the equation in vertex form.
Separate the variable terms from the constant terms:
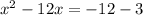
Now we complete squares on the left side of the equation. We use the following algebraic identity:
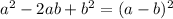
It's evident that the second term of our equation has a value of b = 12/2=6
Thus, we need to complete squares by adding 6 squared = 36 as follows:

Applying the above identity:
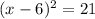
Since this equation is a different expression of the very same original equation, they have both the same solution.
Answer: The last choice (x-6)^2=21