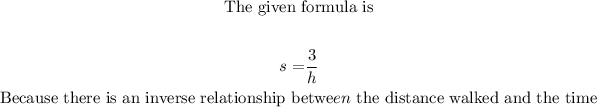
If the number of hours it takes the student to walk home increases, then the speed decreases
Let us see an example
if h = 1
and we increase h to be = 3
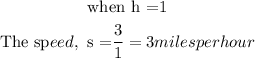
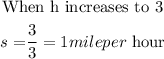
3miles/hour is more than 1 mile/hour so hence the speed will decrease when the time increases
The answer is option A, the speed decreases