Question

Suppose you have an experiment where you toss a fair coin 3 time you didn't count the number of heads observe over those 3 tosses use this experiment to address each of the falling question round solution to 3 destiny places

Answer 1

a) In order to complete the table for the probability distribution for the variable X:

X = the number of heads observed when you flip a coin three times,

b) we create a list of all the possible outcomes. We use the notation: H = heads, T = tails.

The possible outcomes after tossing the coin three times are:

`HHH,HHT,HTH,THH,TTT,TTH,THT,HTT`

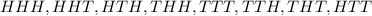
From the list above we see that we have 8 equiprobable events. Now, we classify the events according to the number of Heads included.

- Events with x = #H = 0: TTT

- Events with x = #H = 1: HTT, THT, TTH

- Events with x = #H = 2: HHT, HTH, THH

- Events with x = #H = 3: HHH

Using the data above we compute the probabilities for each x, we simply compute the quotient between the number of outcomes of each case by N = 8 (the total number of possible outcomes):

`\begin{gathered} P\mleft(x=0\mright)=(1)/(8)=0.125 \\ P(x=1)=(3)/(8)=0.375 \\ P(x=2)=(3)/(8)=0.375 \\ P(x=3)=(1)/(8)=0.125 \end{gathered}`

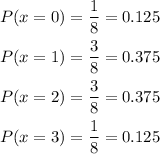
c) Shape of the probability disribution. The probability distribution of x is: Symmetric.

d) Using the data above, we can compute the mean number of heads for the distribution:

`\begin{gathered} E(x)=\sum ^3_(n=0)x_n\cdot P(x_n_{}) \\ E(x)=0\cdot P(x=0)+1\cdot P(x=1)+2\cdot P(x=2)+3\cdot P(x=3) \\ E(x)=0+1\cdot0.375+2\cdot0.375+3\cdot0.125 \\ E(x)=(3)/(2)=1.5 \end{gathered}`

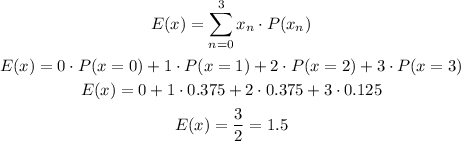
So the mean number of heads for this distribution is 1.5