Question

A bank features a savings account that has an annual percentage rate of r = 5.2% with interest compoundedsemi-annually. Dylan deposits $7,000 into the account.nakThe account balance can be modeled by the exponential formula A = P(1+ where A is the futurevalue, P is the present value, r is the annual percentage rate, k is the number of times each year that theinterest is compounded, and n is the time in years.(A) What values should be used for p, r, and k?PAT =k=(B) How much money will Dylan have in the account in 8 years?Answer = $Round answer to the nearest penny.(C) What is the annual percentage yield (APY) for the savings account? (The APY is the actual or effectiveannual percentage rate which includes all compounding in the year).APY =Round answer to 3 decimal places.

Answer 1

(A) Given that:

Present value, P = $7000

Annual percentage rate, r = 5.2% = 0.052

Number of compounding periods, k = 2

(B) Plug the values into the formula

`A=P(1+(r)/(k))^(nk)`

gives

`A=7000(1+(0.052)/(2))^(2n)`

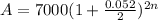
Substitute 8 for n to find the amount of money after 8 years.

`\begin{gathered} A=7000(1+(0.052)/(2))^(2\cdot8) \\ =7000(1.026)^(16) \\ =10554.94 \end{gathered}`

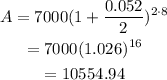
In 8 years, Dylan will have $10554.94 in account.

(C) Find the annual percentage yield using the formula

`\text{APY}=(1+(r)/(k))^k-1`

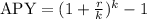
Plug the values into the formula.

`\begin{gathered} \text{APY}=(1+(0.052)/(2))^2-1 \\ =5.268\% \end{gathered}`

The annual percentage yield for the savings account is 5.268%.