Question

Suppose we want to choose 5 objects, without replacement, from 9 distinct objects. If the order of the choices is relevant, how many ways can this be done? If the order of the choices is not relevant, how many ways can this be done?

Answer 1

If the order of choice is relevant, use permutation. We have to choose 5 objects in a total of 9:

`9*8*7*6*5=15120\text{ ways}`

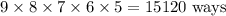
Obs: Initially we have 9 objects, you choose one, then we have 8, you choose another, then you have 7..... (this is the reasoning)

If the order of choice is not relevant, use a combination. This can be done by the equation above:

`C_(9,5)=(9!)/((9-5)!*5!)`
`C_(9,5)=(9!)/(4!*5!)`
`C_(9,5)=(9*8*7*6*5!)/(4!*5!)`
`C_(9,5)=(9*8*7*6)/(4*3*2*1)`
`C_(9,5)=126\text{ ways}`

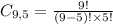
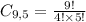
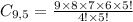
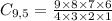
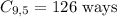
Obs: It is a combination of 9 elements chosen 5 by 5.