Question

If k is the midpoint of CT , CK =3x+23,and KT =5x+7,then find x and CT

Answer 1

Given:

CK = 3x + 23

KT = 5x + 7

If K is the midpoint of CT, then CK = KT. Then,

`3x+23=5x+7`

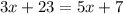
Finding x:

Subtracting 3x from both sides:

`\begin{gathered} 3x+23-3x=5x+7-3x \\ 23=2x+7 \end{gathered}`

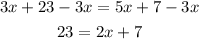
Subtracting 7 from both sides:

`\begin{gathered} 23-7=2x+7-7 \\ 16=2x \end{gathered}`

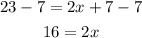
And dividing both sides by 2:

`\begin{gathered} (16)/(2)=(2x)/(2) \\ 8=x \end{gathered}`

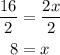
x = 8.

Finding CT:

K is the midpoint of CT, then CT = CK + KT

`\begin{gathered} CT=3x+23+5x+7 \\ CT=3*8+23+5*8+7 \\ CT=24+23+40+7 \\ CT=94 \end{gathered}`

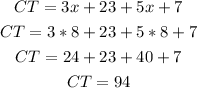
CT = 94.

Answer:

x = 8

CT = 94