Question

Three glasses of milk and 4 snack bars have a total of 80 carbohydrates (carbs), and 4 glasses of milk and 3 snack bars have a total of 81 carbs. Determine how many carbs are in one glass of milk and in one snack bar.

Answer 1

Let m be a glass of milk and s be a snack bar.

3 glasses of milk and 4 snack bars have a total of 80 carbohydrates. So, the expression is,

`3m+4s=80\ldots..(1)`

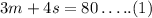
4 glasses of milk and 3 snack bars have a total of 81 carbs.

`4m+3s=81\ldots\ldots.(2)`

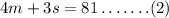
The above equation can be rewritten as,

`\begin{gathered} 4m=81-3s \\ m=(81-3s)/(4)\ldots..(3) \end{gathered}`

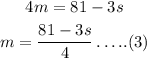
Put equ (3) in (1) to find s.

`\begin{gathered} 3*((81-3s)/(4))+4s=80 \\ (243-9s)/(4)+4s=80 \\ (243-9s+16s)/(4)=80 \\ 243-9s+16s=320 \\ 7s=77 \\ s=11 \end{gathered}`

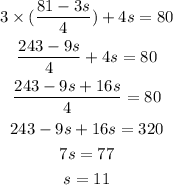
Now, put 11 for s in equ (1) to find m.

`\begin{gathered} 3m+4*11=80 \\ 3m+44=80 \\ 3m=36 \\ m=12 \end{gathered}`

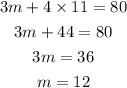
So, there are