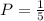Given that:
- A stack of different cards numbered from 1 to 10.
- A card is randomly selected and then replaced. Then another card is randomly selected.
• You need to find the probability that the first card is an odd number.
By definition, Odd Numbers are those numbers that cannot be divided by 2. In this case, these are:
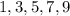
Knowing that the total number of cars is:
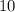
You can set up:
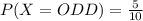
Then:
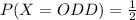
• You need to find the probability that the second card is less than 5.
Notice that the numbers cards from the stack that are less than 5 are:
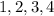
Therefore, you can set up that:
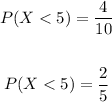
• Now you can set up:
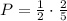
Solving the Multiplication, you get:
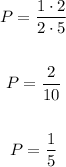
Hence, the answer is: