Solution
Step 1
Use the secant and tangent theorem to a circle.
Step 2
AC = 30 + x
BC = x
CD = 20
Step 3
Substitute into the theorem
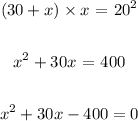
Step 4
Use the factorization method to solve for x.
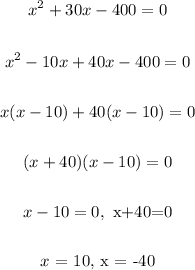
Step 5
The value of x cannot be negative, hence x = 10
Final answer
x = 10