Question

Write a quadratic function in standard form whose graph passes through the given points1. (-1,5), (0,3), (3,9)

Answer 1

The Standard Form of a Quadratic Function:

`\text{ y = ax}^2\text{ + }bx\text{ + c}`

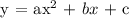
Using the given points (-1,5), (0,3), and (3,9)​, let's substitute each point to the equation.

At (-1,5):

`\text{ y = ax}^2\text{ + bx + c }\rightarrow5=a(-1)^2\text{ + b(-1) + c}`
`\text{ 5 = a - b + c}`

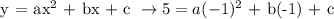
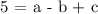
At (0,3):

`\text{ y = ax}^2\text{ + bx + c }\rightarrow3=a(0)^2\text{ + b(0) + c}`
`\text{ 3 = c}`

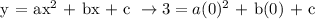
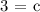
At (3,9):

`\text{ y = ax}^2\text{ + bx + c }\rightarrow9=a(3)^2\text{ + b(3) + c}`
`\text{ 9 = 9a + 3b + c}`

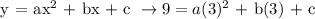
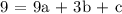
We now get these equations:

5 = a - b + c ; 3 =c; 9 = 9a + 3b + c

Let's determine the value of a, b and c. We get,

Substituting 3 = c to 5 = a - b + c,

`\text{ 5 = a - b + c }\rightarrow\text{ 5 = a - b + 3 }\rightarrow\text{ a - b = 2}`
`\text{ b = a - 2}`

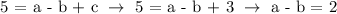
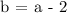
Let's substitute 3 = c and b = a - 2 to 9 = 9a + 3b + c,

`\text{ 9 = 9a + 3b + c }\rightarrow\text{ 9 = 9a + 3(a-2) + 3}`
`\text{ 9 = 9a + 3a - 6 + 3 }\rightarrow\text{ 12a = 9 + 6 - 3 }\rightarrow\text{ 12a = 12}`
`\text{ a = }(12)/(12)\text{ = 1}`

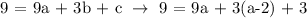
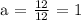
Since a = 1, let's solve for the value of b which is b = a - 2.

`\text{ b = a - 2 }\rightarrow\text{ b = 1 - 2}`
`\text{ b = -1}`

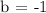
Since we've identified that a = 1, b = -1 and c = 3, let's substitute the values to the standard form of a quadratic function to be able to make the equation.

`\text{ y = ax}^2\text{ + bx + c }\rightarrow y=(1)x^2\text{ + (-1)x + (3)}`
`\text{ y = x}^2\text{ - x + 3}`

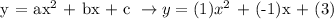
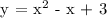
Therefore, the quadratic function in a standard form whose graph passes through the given points (-1,5), (0,3), (3,9)​ is y = x^2 - x + 3.